.ipynb .pdf

repository open issue

Binder

Contents

Correlation and covariance

Correlation and covariance are measures of the degree of relationship between two continuous random variables.

Covariance

Let \(X\) and \(Y\) be two random variables which are not necessarily independent. Then the variance of their sum is found as

\[ Var(X+Y) = E\left(((X+Y)-(E(X)+E(Y)))^{2}\right) \]

This can be written as

\[ E\left(((X-E(X)) + (Y-E(Y)))^{2}\right) \]

which equals

\[ E\left((X-E(X))^{2} + (Y-E(Y))^{2} + 2(X-E(X))(Y-E(Y)) \right) \]

We can now write this as:

\[ Var(X+Y) = Var(X) + Var(Y) + 2E((X-E(X))(Y-E(Y))) \]

We define the covariance between \(X\) and \(Y\) as:

\[ Cov(X,Y) = E\left( (X-E(X)) (Y-E(Y)) \right) \]

From its definition we see that if when \(X-E(X)\) tends to be positive, \(Y-E(Y)\) tends to be positive, then \(Cov(X,Y)>0\). Conversely, if when \(X-E(X)\) tends to be positive, \(Y-E(Y)\) tends to be negative, then \(Cov(X,Y)<0\).

Returning to the equation above, for two random variables \(X\) and \(Y\)

\[ Var(X+Y) = Var(X) + Var(Y) + 2Cov(X,Y) \]

Linear association

Note It is important to remember that covariance is only a measure of linear association. Two variables \(X\) and \(Y\) can be strongly dependent, yet have zero covariance.

Rules of covariance

There are various rules which covariance follows, resulting from its definition in terms of expectations. For example:

• \(Cov(X,X) = Var(X)\)

• \(Cov(X, Y) = Cov(Y, X)\)

• \(Cov(aX, bY) = abCov(X, Y)\)

Try proving the first one for yourself.

And some slightly more complex rules (for reference):

• \(Cov(aR+bS,cX+dY) = acCov(R,X) + adCov(R,Y) + bc Cov(S,X) + bd Cov(S,Y)\)

• \(Cov(aX+bY,cX+dY) = acVar(X) + bdVar(Y) + (ad+bc)Cov(Y,X)\)

• \(Cov(X + Y, X - Y) = Var(X) - Var(Y)\)

Correlation

The size of \(Cov(X,Y)\) depends on the scale/magnitude of variability of \(X\) and \(Y\). The correlation between \(X\) and \(Y\) is a standardised version of the covariance.

\[ Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}. \]

We can take the square root of the variance of \(X\) and \(Y\) to get their standard deviations, \(SD(X) = \sqrt{Var(X)}\) and \(SD(Y) = \sqrt{Var(Y)}\). Then we can also write:

\[ Corr(X,Y) = \frac{Cov(X,Y)}{SD(X)SD(Y)}. \]

• The correlation coefficient lies between -1 and 1.

  • \(Corr(X,Y)=1\) or \(Corr(X,Y)=-1\) means \(X\) and \(Y\) are perfectly correlated.

  • However, it is important to remember that this does not necessarily mean \(X\) and \(Y\) are equal.

  • For example, if \(Y=2X\), they have correlation 1 but are not equal to each other.

• \(Corr(X,Y)=0\) does not mean \(X\) and \(Y\) are independent.

  • It is possible for two variables to be strongly dependent (associated) yet have zero correlation.

  • As for covariance, correlation is a measure of linear association

  • However, if \(X\) and \(Y\) are independent then \(Corr(X,Y)=0\).

Example

In the figure below, try to guess what the correlation between the two variables is. Once you’ve had a think, click the button on the right to see the correct values.

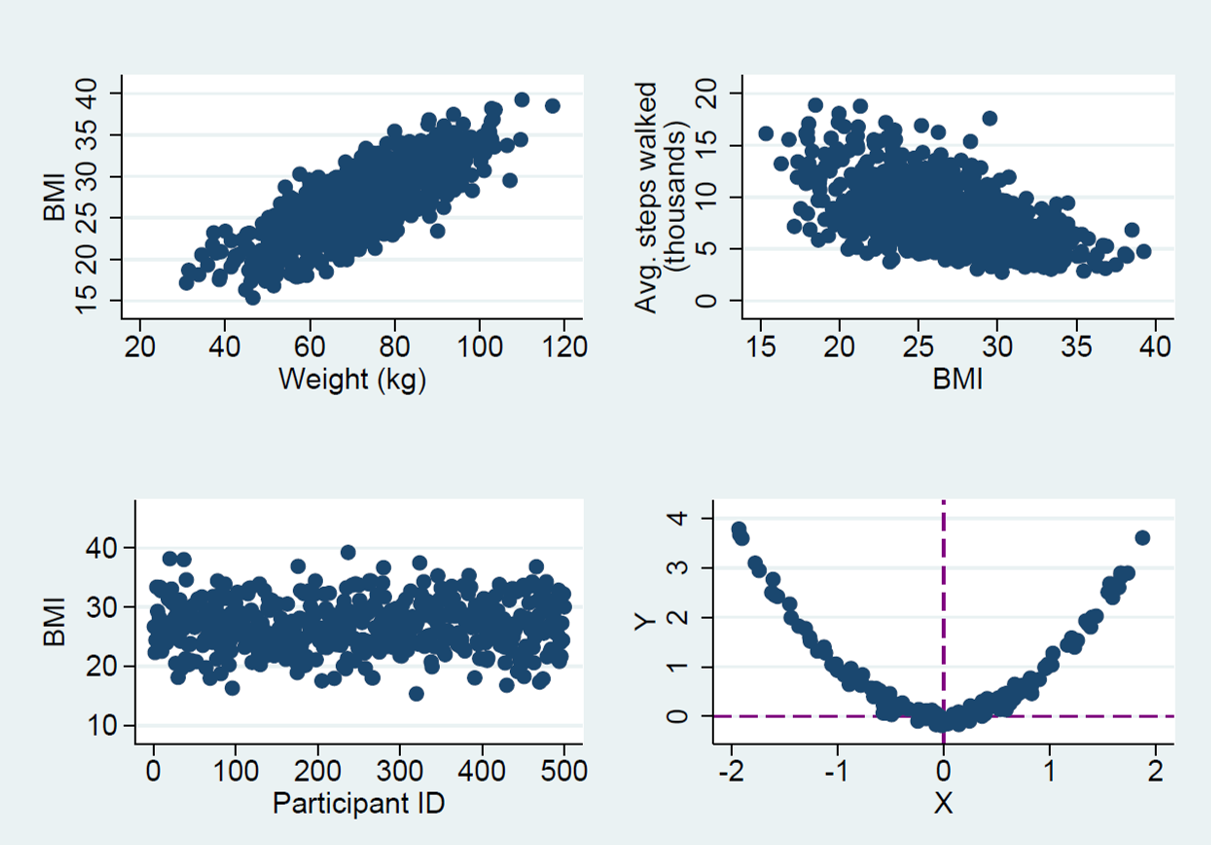
Fig. 6 Examples of correlation between variables

Answers:

• top left 0.8 - strong positive correlation

• top right-0.55 - moderately strong negative correlation

• bottom left 0.001 - no relationship, no correlation

• bottom right -0.07 - strong dependence but no linear association so no correlation

Continuous Random Variables Distributions