Probability and statistics¶
We assume that students are already familiar with the basic probability concepts covered in the pre-course Refresher.
How does probability relate to statistics?¶
Probability theory describes the chance of an event occurring while statistics concerns the collection, organization, analysis and interpretation of data. However, probability theory and statistics are intrinsically linked.
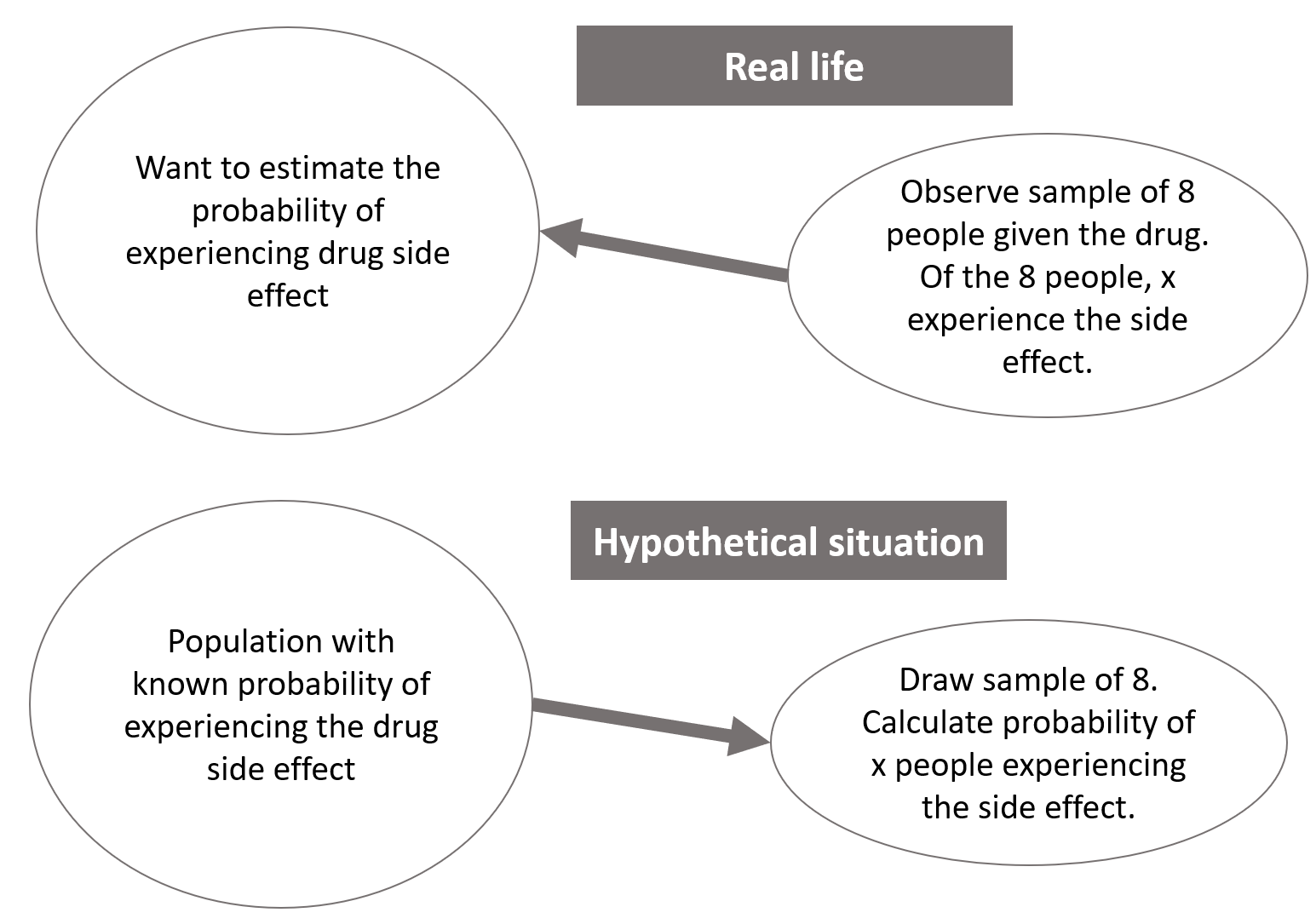
A typical probability problem is as follows. We are planning to run a small clinical study, which involves giving 8 patients a particular drug. We are told that the probability that a single patient experiences a side effect from a particular drug is 0.23. From this information, we can calculate the probability of various complex events occurring. For example, we might want to know the probability that more than 6 of the 8 patients will experience a side effect. Or we might wish to know the probability that none of the 8 patients experience a side effect. Here, we are assuming that a characteristic (parameter) of the population is known. Specifically, we are assuming that we know the true probability of a single patient experiencing a side effect.
This is not how real life works! Typically, in health data science studies, we have observed some data which we believe can be modelled using a particular distribution (such as the binomial distribution that we will soon meet), but the parameters of that distribution are unknown. For the small clinical study, for example, in real life we would run the study and observe how many of the 8 patients did in fact experience a side effect. But the probability of a patient experiencing a side effect would be unknown. The study aim would be to use the observed data to make statements - inferences - about this unknown probability. So in some senses, the problem is the opposite way round.
It turns out that the process of statistical inference relies very heavily on probability calculations. Suppose we conduct our small clinical study and, for example, observe that in fact 2 of the 8 patients experience the side effect. Loosely speaking, the process of inference involves the following steps. We use probability theory to calculate the probability that 2 people within our sample of 8 experience the side effect, for every possible value of the unknown probability of experiencing a side effect. We then use these probabilities to make statements about plausible values of the unknown probability. As we will see, we can take various approaches to this inference, in particular using the frequentist or Bayesian frameworks.
Therefore, the next two lectures, concerning probability theory, comprise building blocks that you will need when you subsequently meet ideas about likelihood, inference and regression modelling.