9.6 Summarising Posteriors¶
We often display the posterior distribution graphically to get a sense of the information that we have about the parameter. However, other ways to summarize the distribution can be helpful. We may also wish to summarise the posterior distribution by a credible interval.
Remember that a classical 95% confidence interval is defined such that, if the data collection process is repeated again and again, then in the long run, 95% of the confidence intervals formed would contain the true parameter value.
A Bayesian 95% credible interval is an interval which contains 95% of the posterior distribution of the parameter.
There may be several different credible intervals such that the interval contains 95% of the distribution. The 95% Highest Posterior Density (HPD) interval is the credible interval with the smallest range of values for \(\theta\) (providing the posterior is concave). Algebraically, this is the region \([\theta_L, \theta_U]\) that contains \(95\%\) of the probability, such that:
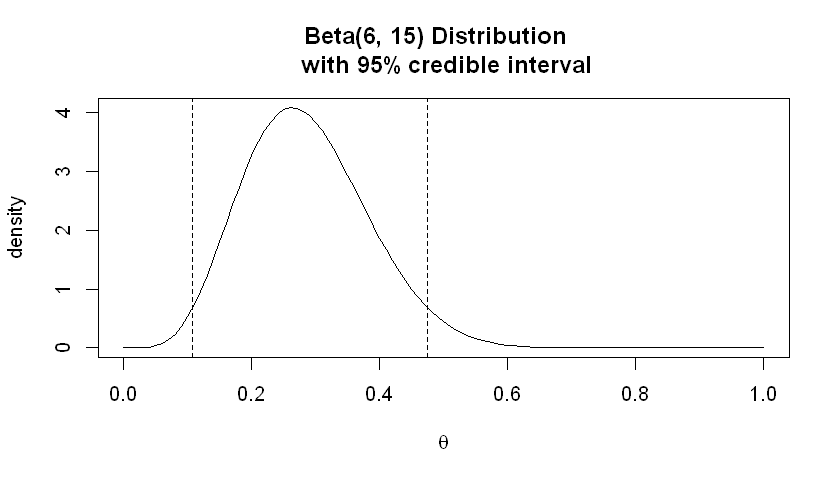
In our previous example, when we used the asymmetrical \(Beta(2, 9)\) prior, our posterior was \(Beta(6, 15)\). The posterior mean is \(\frac{6}{6+15}=0.286\). The 95% HPDI is (0.107,0.475). We plot the distribution below and check that the area between these two values gives us 0.95. Now, note that the interval (0.09, 0.465) also gives us an area of 0.95, but this interval is wider. In a sense, the HPDI is the “tightest” interval so that the area under the posterior distribution is 0.95.
p <- seq(0, 1, 0.01)
options(repr.plot.width=7, repr.plot.height=4)
plot(p, dbeta(p, 6, 15), type="l", main="Beta(6, 15) Distribution \n with 95% credible interval", xlab=expression(theta), ylab="density")
abline(v=0.475, lty="dashed")
abline(v=0.107, lty="dashed")
#Area under the 95% HDPI
pbeta(0.475, 6, 15)-pbeta(0.107, 6, 15)
#The interval (0.09, 0.465) also a 95% credible interval
pbeta(0.465, 6, 15)-pbeta(0.09, 6, 15)
Note:
We have phrased the above discussion in terms of 95% confidence and credible intervals. However, there is nothing special about the level 95%. We can make the discussion more general by talking about \(100(1−𝛼)\%\) confidence or credible intervals instead, with \(\alpha \in (0,1)\) (where \(\alpha = 0.05\) for 95% confidence or credible intervals but e.g. \(\alpha = 0.01\) for 99% intervals).
