5.3 Log likelihood¶
We have discussed the idea that finding the maximum value of a likelihood gives us sensible estimates for the unknown parameters. For the examples above it is relatively clear from calculating a few values of the likelihood where the maximum lies, but this will not always be the case.
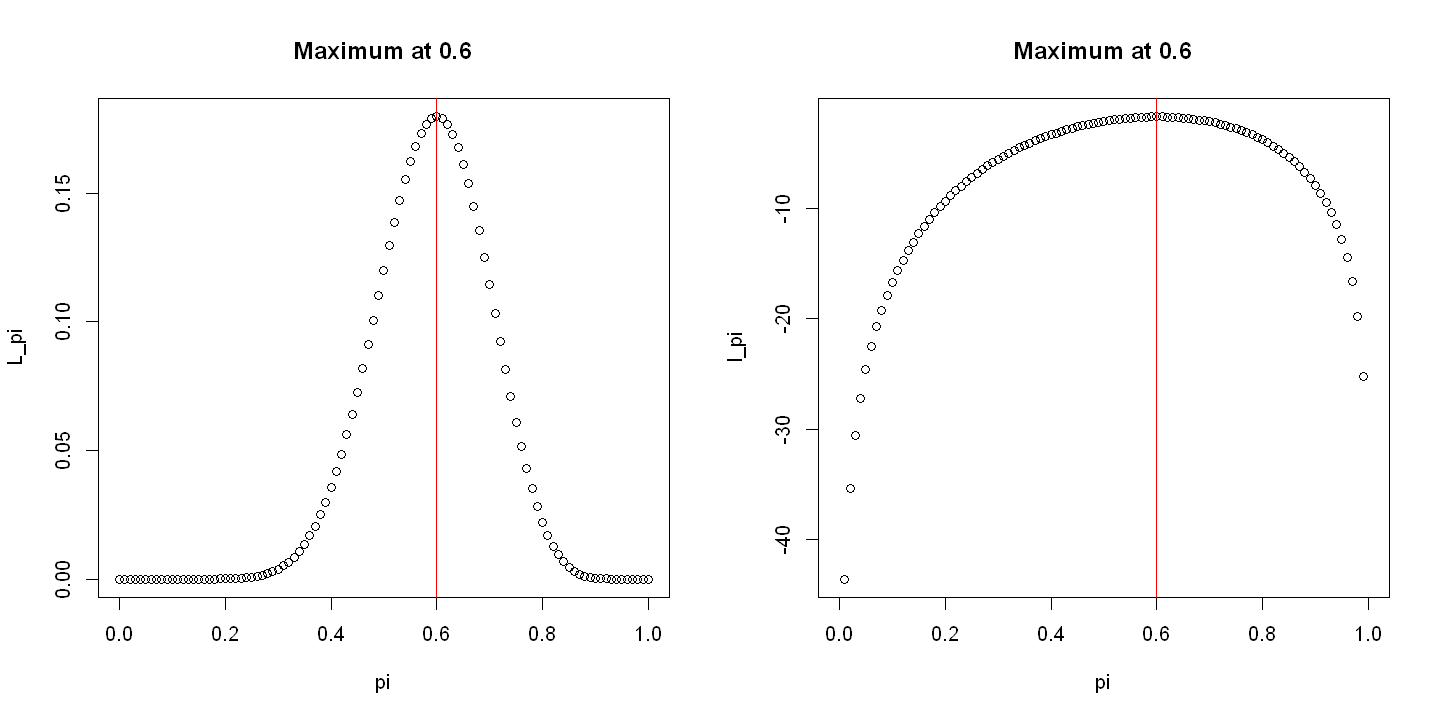
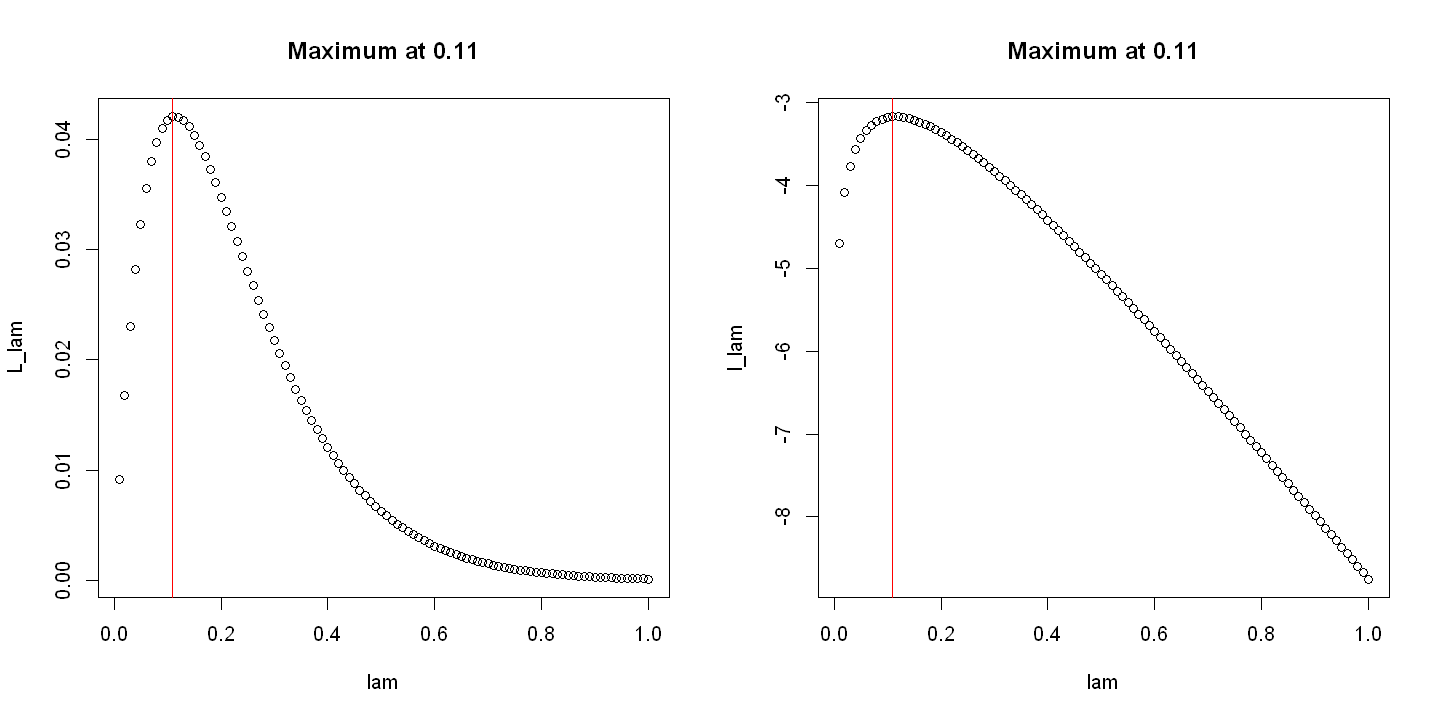
A theoretical result which will come in handy is that a value which maximises the likelihood also maximises the log-transform of the likelihood, or the log-likelihood. This is because the log is a concave function, so when we use it to transform the likelihood, any maximum or minimum stays in the same place on the x-axis. We will denote the log-likelihood by \(l(\theta) = \log(L(\theta))\).
This result is evident when plotting the transformation of the likelihoods for the binomial and exponential distributions.
For the binomial example:
options(repr.plot.width=12, repr.plot.height=6)
par(mfrow = c(1,2))
# likelihood L(pi)
pi = seq(0,1,by = 0.01)
L_pi <- choose(20,12)*pi^12*(1-pi)^(20-12)
pi_max <- pi[which.max(L_pi)]
plot(x = pi, y = L_pi)
abline(v = pi_max, col = "red")
title(paste("Maximum at", pi_max))
# log-likelihood l(pi)
l_pi <- log(L_pi)
plot(x = pi, y = l_pi)
abline(v = pi[which.max(l_pi)], col = "red")
title(paste("Maximum at", pi[which.max(l_pi)]))
For the exponential example:
options(repr.plot.width=12, repr.plot.height=6)
par(mfrow = c(1,2))
# likelihood L(beta)
lam = seq(0.01,1,by = 0.01)
L_lam <- lam*exp(-8.75*lam)
lam_max <- lam[which.max(L_lam)]
plot(x = lam, y = L_lam)
abline(v = lam_max, col = "red")
title(paste("Maximum at", round(lam_max,2)))
# log-likelihood l(beta)
l_lam <- log(L_lam)
plot(x = lam, y = l_lam)
abline(v = lam[which.max(l_lam)], col = "red")
title(paste("Maximum at", round(lam[which.max(l_lam)],2)))
5.3.1 Why use the log likelihood?¶
Log-transformed likelihoods are generally “better-behaved” and easier to work with than the original form. Remember the rules of logs for products and powers - we’ll see in the next section how these make computation with the log-likelihood very convenient.
